Richard F. Hassing
On Aristotelian, Classical
and Quantum Physics (2003)
Link to the original text:

Newton, William Blake
This article was uploaded to the Institute for the Study of Nature (isnature.org) webpage. Professor Richard Hassing is a researcher at the Catholic University of America, and one of his main interests is the history of Physics and the Philosophy of Nature. I consider this text to be an excellent approach to the amazing subject of physics and its intimate link to philosophy. You may find more information about professor Hassing’s work at his university profile (https://philosophy.catholic.edu/faculty-and-research/faculty-profiles/hassing-richard/index.html). I would like to thank him for his cordiality and for allowing me to translate this article.
Sobre las físicas aristotélica, clásica y cuántica
Prefacio
El límite entre el deseo y la elección está definido por las limitaciones de nuestras capacidades. Como dice Aristóteles, podemos desear “cosas imposibles, por ejemplo, la inmortalidad [corporal]”, pero siempre elegimos aquello de lo que, a nuestro juicio, somos capaces [1].
Las diferentes explicaciones de la naturaleza física —y en particular las diferentes explicaciones de la relación entre lo sensible y lo inteligible— acarrean distintas consecuencias respecto de qué está a nuestro alcance y, por lo tanto, distintas consecuencias para nuestro patrón de decisiones en la vida y las disposiciones relacionadas de la voluntad y el apetito [2, 3, 4]. Esta es la relevancia de la filosofía moderna temprana y su fruto, la física clásica. En Bacon y Descartes, y en forma definitiva en Newton, las leyes de la naturaleza reemplazan a las formas y los fines naturales como inteligibles fundamentales de la ciencia física, y comportan una gran expansión de la capacidad humana para predecir, controlar, transformar los procesos naturales: para la prolongación de la vida y “el alivio de la condición humana”1. La fase final de este proyecto es la genética y sus posibilidades aparentemente radicales para transformar la vida humana. Incluso se habla sobre alcanzar la inmortalidad corpórea2: algo imposible según la ciencia biológica aristotélica de la forma orgánica, o alma, y su correlato, la materia corrompible por necesidad.
A causa de estas relaciones entre los tipos de física y sus consecuencias (reales o imaginarias [5]) en torno a los límites de nuestra capacidad, nuestros patrones de decisión, las disposiciones correspondientes de la voluntad, el apetito y la imaginación, y las concepciones del mundo resultantes, dudo que sea posible separar por completo la metafísica y la filosofía de la naturaleza de la ética3. Esto es en particular problemático hoy en día, debido a la dificultad de discernir las limitaciones esenciales de la ciencia natural moderna.
Introducción
Las librerías ofrecen bastantes obras sobre la extrañeza de la física cuántica. Hasta donde sé, no existe ningún libro sobre la extrañeza de la física clásica, a la que los físicos incluso describen como sentido común aguzado. No creo que esto sea así, por lo que el tema central y el título más indicado para esta conferencia sería “La extrañeza clásica”.
Mi intención es analizar la física clásica ante un público familiarizado con el enfoque aristotélico, un público que, por lo tanto, es capaz de apreciar el contraste marcado entre la filosofía moderna temprana y la física clásica, por un lado, y la física aristotélica, por el otro. Destacaré, en particular, una disposición y cosmovisión paradójica e inmoderada que se asocia con la física clásica, disposición que alcanza a la genética contemporánea, a pesar de las enormes diferencias entre la biología y la física clásica.
La cosmovisión de la física clásica se puede apreciar en el modelo universal newtoniano de fuerzas y partículas. Pero ciertas características básicas de este modelo newtoniano se hallan, más en general, en toda la física precuántica, incluso en la física de Einstein, el detractor más elocuente de la física cuántica. Así, por “física clásica” entiendo a toda la física matemática posaristotélica y precuántica, incluida la relatividad. Trataré sobre la física cuántica de manera más bien indirecta, por medio de comparaciones breves e insuficientes con las físicas aristotélica y clásica. En el contexto de la física clásica, la física cuántica parece ser, en efecto, un giro radical. Sin embargo, como destaqué, sostengo que la física clásica es en sí un quiebre radical con respecto a la física aristotélica precedente. Esto no quiere decir que la filosofía natural aristotélica pueda darnos sin más una comprensión filosófica adecuada de la física cuántica. El fenómeno cuántico de la no localidad o entrelazamiento [62] presenta un desafío para cualquier filosofía de la naturaleza. Pero yo creo que el enfoque aristotélico es valioso, quizás indispensable, para la futura comprensión de cuál es el significado real de la mecánica cuántica.

Louis-Victor de Broglie
Sobre la física clásica
Louis de Broglie presenta con claridad algunas cuestiones básicas sobre la física clásica en una recopilación de ensayos de 1955, bajo el título Physics and Microphysics. El extenso fragmento que leeré a continuación describe algunas características comunes a las tres grandes teorías de la física clásica (la mecánica, el electromagnetismo y la termodinámica), así como de la relatividad einsteniana. De hecho, las consideraciones que haré sobre este pasaje serán esenciales para la concepción de Einstein sobre la física. Esta concepción, basada en la física clásica, se opone a la física aristotélica, por un lado, y a la física cuántica, por otro lado. Esta es la descripción de la física clásica de de Broglie [58]:
Con las coordenadas [cartesianas] de espacio y tiempo, la física matemática clásica estaba en condiciones de representar de manera precisa la sucesión de fenómenos que nuestros sentidos nos permiten verificar a nuestro alrededor.
Desde ese momento, se abrió con mucha naturalidad un camino ante a la física teórica, por el que transitó audaz. Se creía que toda evolución del mundo físico debía estar representada por cantidades [por ejemplo, la posición y el momento de una partícula] localizadas en el espacio y variables a lo largo del tiempo. Estas cantidades debían posibilitar la descripción completa del estado del mundo físico a cada instante y, por lo tanto, la descripción de toda la naturaleza por medio de cifras y movimientos, según el programa de Descartes. Aquello se llevaría a cabo en su totalidad con la herramienta de las ecuaciones diferenciales (…) que nos permitieran seguir la ubicación y la evolución a lo largo del tiempo de todas las cantidades que definen el estado del mundo físico. ¡Una concepción magnífica por su simplicidad y confirmada por los éxitos que obtuvo durante tanto tiempo! [Deberíamos preguntarnos si alguna vez ocurrieron tales éxitos en la biología.] Sostuvo y orientó todos los esfuerzos de las grandes corrientes de física matemática del siglo XIX.
Sin dudas, no todos los científicos adherían de la misma manera a esta descripción del mundo por medio de cifras y movimientos. Algunos con una imaginación vivaz y concreta buscaron representar los elementos del mundo material de manera que los fenómenos que observan nuestros sentidos surgieran a partir de la existencia y el movimiento de átomos o corpúsculos demasiado pequeños para ser observados directamente; pretendían desmantelar la maquinaria para ver todos los engranajes en funcionamiento. Otros, más cautos y, sobre todo, dotados de una mente más abstracta, pretendían contentarse con solo representar los fenómenos por medio de cantidades directamente medibles y desconfiaban de las hipótesis (a sus ojos, demasiado especulativas e inútiles) de los atomistas. Y si bien los atomistas avanzaban con intrepidez, abrían nuevos caminos y permitían que la ciencia gozara de un progreso asombroso, los energistas, impedidos por sus métodos más formales y cautos, retenían cierta ventaja desde el punto de vista conceptual cuando criticaban los aspectos más simplistas e ingenuos de las representaciones que proponían sus audaces rivales. Pero, sin ser conscientes de ello, ambos [los atomistas y los energistas] aceptaban ciertos (…) postulados comunes que el futuro habría de probar endebles.
De hecho, estaban de acuerdo en admitir la validez de la estructura abstracta del espacio y el tiempo, la posibilidad de seguir la evolución del mundo físico gracias a cantidades ubicadas con precisión en el espacio que variaran continuamente a lo largo del tiempo y la legitimidad de describir todos los fenómenos por medio de conjuntos de ecuaciones diferenciales. Aunque los energistas, como Pierre Duhem, se negaban a admitir la intervención ubicua de un “movimiento local” que se pudiera representar a través de un desplazamiento de partes, afirmaban sin más la consideración de “movimientos generales” definidos de manera más abstracta por las variaciones de cantidades a lo largo del tiempo. A pesar de sus diferencias de opinión sobre cómo implementar este programa, todos los teóricos estaban de acuerdo, entonces, en representar el universo físico con cantidades bien definidas en espacio y tiempo y sujetas a ecuaciones diferenciales.
Las ecuaciones diferenciales (…) de la física matemática clásica tienen el carácter común de permitirnos seguir rigurosamente toda la evolución de los fenómenos que describen, si suponemos la existencia de ciertos datos conocidos relativos a un estado inicial que se corresponda con un valor de tiempo particular. De allí se dedujo la posibilidad de establecer una cierta interconexión inevitable de todos los fenómenos y se llegó, por lo tanto, a la concepción de un determinismo universal de los fenómenos físicos. No me propongo evaluar la idea del determinismo universal desde el punto de vista filosófico ni necesito preguntarme a mí mismo, por ejemplo, si la mente, que al fin y al cabo es la creadora de la física matemática, podría recuperar su lugar en una naturaleza concebida de manera tan rígida. Lo indudable es que los fenómenos físicos, tal como se los representaba con exactitud por medio de las ecuaciones diferenciales de la física clásica, estaban sujetos a un determinismo definido de manera sumamente precisa.
La física clásica representaba así la totalidad del universo físico tal como se lo proyectaba con precisión absoluta en el marco del espacio y el tiempo, a partir del que evolucionaba de acuerdo con leyes de necesidad inexorable. Hacía a un lado por completo los medios utilizados para obtener un conocimiento de las distintas partes de este vasto mecanismo, ya que, si bien reconocía la existencia de errores experimentales, solo veía en ellos el resultado de una falta de precisión en nuestros sentidos y de la imperfección de nuestras técnicas [experimentales], y aceptaba la posibilidad de reducirlos indefinidamente, al menos en principio, gracias al perfeccionamiento adecuado de nuestros métodos. Todas estas representaciones se basaban, en esencia, en las ideas clásicas del espacio y el tiempo; durante mucho tiempo parecieron bastar para describir la evolución del mundo material. (Physics and Microphysics, 116-18)
De este fragmento extenso, tomo tres características de toda la física clásica, que también dan cuenta de una idea sobre la relación entre mente y mundo, o intelecto y naturaleza. Las tres características son:
- Continuidad del espacio, el tiempo y el movimiento
- Representabilidad espaciotemporal de los procesos fundamentales
- Causalidad determinista
En primer lugar, por continuidad del espacio, el tiempo y el movimiento se entiende, por ejemplo, que sería absurdo que un planeta modificara su distancia respecto del Sol al desaparecer repentinamente de su posición actual y reaparecer al instante en una nueva posición en una órbita con un radio diferente. Las órbitas de los planetas son continuas; no existen saltos. En segundo lugar, por representabilidad espaciotemporal de los procesos fundamentales se entiende que, para nuestra imaginación matemática, siempre es posible asignar coordenadas espaciales cartesianas (x, y, z) y luego representar las cantidades físicas relevantes que varían en ese espacio con el tiempo. Imaginemos, por ejemplo, una partícula con una posición, x(t), y un momento, p(t), precisos que se mueve en su trayectoria. Se presume que esta manera de utilizar la mente se adecúa por completo a la naturaleza de las cosas. En tercer lugar, por causalidad determinista se entiende que, por medio de las ecuaciones de movimiento, los valores numéricos de las cantidades relevantes en un instante de tiempo nos permiten calcular los valores de esas cantidades en el próximo instante y en el próximo y así sucesivamente. No se necesita de ningún otro tipo de causalidad, más allá de los datos iniciales (o condiciones de frontera) y las ecuaciones de movimiento, para explicar todos los fenómenos naturales.
Esta grandiosa concepción complementa una idea de realismo científico que Einstein expresó con mucha sencillez: “La creencia en un mundo externo independiente del sujeto que lo percibe es la base de toda la ciencia natural” [60]. En cierto sentido, esto es harto plausible: ¿la luna está allí cuando nadie la mira? Por supuesto que sí. Pero en otro sentido más filosóficamente preciso, la afirmación de Einstein es muy problemática; basta considerar su uso de los términos “ciencia”, “percibe”, “natural” y, en especial, “externo”, tal como los entiende Aristóteles4. Sea como fuere, bajo esta concepción clásica del mundo físico y su accesibilidad a la mente humana, se presume que las cantidades físicas (como la posición, el momento, la energía, la intensidad de campo) que descubrimos al implementar nuestra física no reciben su ser ni se actualizan de manera alguna a través de nuestros actos de medición, así como la posición de la luna o la intensidad del campo magnético de la Tierra no reciben su ser al ser observados o medidos.
Ilustraré la concepción clásica del mundo al revisar la lógica básica del cálculo de trayectoria newtoniano de un cuerpo que se mueve bajo la fuerza gravitacional. Esto servirá de ejemplo a la explicación de de Broglie y nos introducirá al modelo universal newtoniano de fuerzas y partículas, una cosmovisión con repercusiones notables.
Lógica básica del cálculo de trayectoria newtoniano
Comenzamos el cálculo con la segunda ley del movimiento de Newton, F = mdv/dt, y su ley de la fuerza de gravitación universal, F = -GMm/r2. El problema por resolver es el siguiente: dada por observación empírica la posición, r0, y la velocidad, v0, de un planeta o cometa respecto del Sol en un tiempo determinado, t0, se debe obtener la posición y la velocidad, r1, v1, en un tiempo posterior, t1, sin recurrir a la observación. (Sigo en esencia la explicación de Einstein e Infeld, The Evolution of Physics, p. 30). Entonces, tomamos una hoja grande de papel cuadriculado y representamos en ella el Sol, de masa M, y el planeta o cometa, de masa m, en el tiempo t0:
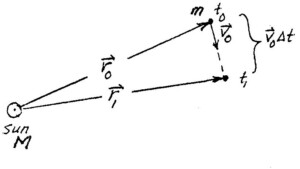
Se muestran los datos iniciales, r0, v0, como flechas o vectores. Si se conoce v0, es posible estimar la posición del planeta o cometa en un tiempo cercano posterior al tiempo t1 si se considera su movimiento como rectilíneo (aunque en realidad sea
curvilíneo). Esto es un error, pero podemos reducirlo tanto como deseemos haciendo que el intervalo ∆t = t1-t0, sea más y más pequeño. Entonces, movemos el planeta o cometa en la dirección de v0 una distancia v0∆t. A partir de los datos iniciales, r0, v0, se obtuvo la posición aproximada del cuerpo en el tiempo t1.
¿Cuál es la nueva velocidad, v1? Por supuesto, un planeta o cometa bajo la atracción gravitacional del Sol se mueve en forma de curva (debe ser así, por la primera ley de Newton). Así, la dirección del vector de velocidad está en cambio constante. Para estimar la nueva velocidad, v1, en el tiempo t1, debemos hallar el cambio de velocidad del cuerpo, ∆vo1, que ocurrió durante el primer intervalo, ∆t, de t0 a t1. Luego, se puede construir, por suma de vectores, v1 = v0 + ∆v01. Así se completaría la predicción de la nueva posición y velocidad del planeta o cometa en un tiempo futuro cercano , ∆t. Esto puede parecer un paso pequeño, porque ∆t es pequeño, pero si se repite para el próximo intervalo, de t1 a t2, y se obtiene r2 y v2 a partir de r1 y v1, y así ad infinitum, entonces habremos logrado una revolución histórica en el pensamiento humano. Aquí es donde cobra valor la ley de gravitación universal de Newton; es el vínculo esencial en la lógica del cálculo de la trayectoria, sin el cual nuestro procedimiento se detendría luego de estimar r1.
Combinar la ley de gravitación con la segunda ley de movimiento permite calcular (de manera aproximada) el cambio de velocidad, ∆vo1:
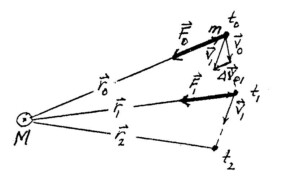
-GMm/r02 = m∆vo1/∆t, entonces ∆v01 = -GM∆t/r0, tal como se muestra. Por lo tanto, tenemos v1 = v0 + ∆v01. Se pudo predecir entonces r1 y v1 a partir de r0 y v0. Podemos repetir este algoritmo: a partir de F1 = – GMm/r12 se obtiene ∆v12 y luego se construye v2 = v1 + ∆V12, al graficar r2, v2, en el tiempo t2, etc. Luego, trazamos la órbita o trayectoria del cuerpo que se mueve bajo la fuerza gravitacional del Sol, sin recurrir a datos observacionales. Tras hacer los cálculos, nos preguntamos: ¿coincide la predicción con las observaciones futuras? Por ejemplo, ¿aparece el cometa Halley donde predijimos que aparecería? Dentro de los límites de precisión observacional, sí.
En esta explicación del concepto de trayectoria, no consideré ciertos detalles técnicos (no linealidad, el problema de los muchos cuerpos, consideraciones sobre la energía) que influyen en el análisis de la trayectoria para poder mostrar aquello que es esencial para el tipo de pensamiento característico de la física clásica. Quisiera remarcar dos características de esta visión newtoniana que de Broglie no comenta de manera explícita y que son de suma importancia para la filosofía de la naturaleza, a saber, (1) la neutralidad específica y (2) lo que denomino el “secularismo” fisicomatemático, a falta de un término mejor5.

Sir Isaac Newton
Neutralidad específica, un nuevo tipo de relación entre lo sensible y lo inteligible
Es importante apreciar el carácter notable de la ley de fuerza gravitacional de Newton [51]. Por lo general, la manera en la que se mueve o se comporta un cuerpo guarda una relación intrínseca con el tipo o especie de cuerpo que es, tal como sabemos por percepción sensible común. Los cerdos no vuelan, los gorriones no guarrean. El antiguo nombre de esta idea es hilemorfismo: “una forma diferente precisa de una materia diferente” [18]. Pero la ley de gravitación no es así; no es como el tipo de relación aristotélica específica entre lo sensible y lo inteligible. La ecuación F = -GMm/r2 expresa un principio inteligible de movimiento local en la naturaleza que es indiferente o neutral con respecto al tipo, tamaño, forma, estructura interna y función de dos cuerpos que interactúan. Es por eso que, en tanto que los cuerpos con extensión espacial en un sistema gravitacional no entren en contacto, se pueden representar matemáticamente como puntos inextensos: puntos de masa. Cabe recordar que, según Aristóteles, en Física 6.4, el ente móvil, el movible per se, es por necesidad divisible [8]. Un punto indivisible e inextenso, por lo tanto, solo puede ser movido per accidens al estar en algo que sea en sí mismo movible per se y, por ende, extenso. Pero en la física de los sistemas gravitacionales, no hace falta esta idea de la filosofía natural para solucionar varios problemas. La extensión espacial, las formas y tamaños de los cuerpos tampoco son relevantes. Como dice Newton, “la Naturaleza es sumamente simple y consistente consigo misma. Cualquier razonamiento que concierna a los movimientos mayores [por ejemplo, del sistema solar] también debe concernir a los menores [de las partículas]” [52].
La peculiar neutralidad específica o estructural de la ley de fuerza gravitacional da lugar a la gran analogía de Newton —todo cuerpo es como un sistema solar a pequeña escala—, por la que generaliza, a partir de su teoría gravitacional particular del modelo universal de fuerzas y partículas, una imagen mental de todo lo físico en el universo entero. Newton propone lo siguiente en el prefacio de sus Principia [53]:
A partir de los fenómenos celestiales, obtengo las fuerzas de gravedad por las que los cuerpos tienden al Sol y a los diversos planetas. Luego, a partir de estas fuerzas (…) deduzco los movimientos de los planetas, los cometas, la Luna y el mar. Mi deseo es conocer el resto de los fenómenos de la Naturaleza a través del mismo tipo de razonamiento basado en principios mecánicos, en tanto que diversas razones me llevan a sospechar que todos ellos [¡!] dependen de ciertas fuerzas por las que las partículas de los cuerpos, por causas hasta ahora desconocidas, se impelen mutuamente una hacia la otra y convergen (…), o bien se repulsan y retroceden (…). Al ignorar estas fuerzas, hasta ahora los filósofos han intentado en vano investigar la Naturaleza.
Aquí, todos los cuerpos que son compuestos y sensibles se conciben mentalmente como cúmulos de partículas subsensibles que se mueven en el espacio según trayectorias calculables (al menos en principio). El presupuesto central aquí es que todos los principios de los fenómenos naturales serán como la ley de fuerza gravitacional: expresables en términos inespecíficos como masa y como relaciones espaciales de centros de atracción y repulsión asimilables a puntos. De más está decir que el descubrimiento de la carga eléctrica y la ley de Coulomb, parecida en su forma algebraica a la de Newton, dieron un gran impulso al programa newtoniano. Así, en 1847, Helmholtz proclamó que el objetivo de la ciencia física era la plena penetración intelectual de la naturaleza por la mente humana [57]:
Los fenómenos naturales deben relacionarse con movimientos materiales a partir de fuerzas motrices invariables, fuerzas que solo dependan de relaciones espaciales (…). Sin embargo, la fuerza que dos masas enteras ejercen entre sí debe resolverse en las fuerzas de todas sus partes entre sí; por tanto, la mecánica se refiere a las fuerzas de puntos materiales, es decir, de puntos espaciales ocupados por materia (…). Por último, la tarea de las ciencias naturales físicas debe ser la siguiente: reducir los fenómenos naturales a fuerzas de atracción y repulsión invariables cuya magnitud dependa de la distancia. La factibilidad de esta tarea es, al mismo tiempo, condición para una plena comprensibilidad de la naturaleza. (“On the Conservation of Force”, Wissenschaftliche Abhandlungen, Vol. I, pp. 15-16)
Según esta concepción del mundo, cada todo en la naturaleza está compuesto por partículas que obedecen leyes de fuerza expresables en términos matemáticos y análogas a la ley de gravitación de Newton. Todas las propiedades y actividades de cada todo en la naturaleza se pueden obtener a partir o en cierta forma son consecuencia de los movimientos locales y las propiedades cuantitativas de sus partículas constituyentes. Por ende, la masa, la carga, las leyes de fuerza asociadas, la posición de las partículas, la velocidad, el momento, la energía, las densidades y fluidos asociados, etc., son los términos adecuados para la explicación de todo fenómeno natural.
¿Qué consecuencias tiene el modelo del universo de fuerzas y partículas, según su propia lógica interna, para la naturaleza tal como la conocemos de manera ordinaria y precientífica? Esta es una lista de doce consecuencias paradójicas, consecuencias que chocan con nuestra experiencia ordinaria basada en la percepción sensible y lo que creemos sobre las cosas naturales, en especial los seres vivos:
- Los todos son reductibles a partes o partículas de simpleza suficiente.
- No existe ningún sentido en el que las partes sean una potencia en el todo.
- El único movimiento real en la naturaleza es el movimiento local de partículas.
- No existe una génesis verdadera, ninguna novedad real en la naturaleza, ningún cambio sustancial.
- Las cualidades secundarias, como los colores, no tienen en sí realidad extramental.
- No existe una unidad intrínseca en los compuestos naturales, solo son conjuntos.
- No existe una estabilidad intrínseca en los tipos de cuerpos naturales y visibles.
- No existe una escala de tamaño intrínseca en la naturaleza.
- No existen momentos o estados privilegiados en la naturaleza, no existen los fines.
- La irreversibilidad temporal de lo que vemos no es un aspecto fundamental de la naturaleza.
- La naturaleza es en principio enteramente comprensible para la mente humana.
- La naturaleza es absolutamente maleable: un tipo de cuerpo se puede transformar en otro [54].
Todas estas nociones entran en conflicto con la comprensión aristotélica de la naturaleza, tal como se puede ver en las citas 7-30 o en cualquier curso sobre Aristóteles. Quiero centrarme en la última noción de la lista: el transformismo. ¿Cómo se sigue del modelo universal de fuerzas y partículas? Es muy sencillo. Si los principios inteligibles son inespecíficos, entonces la heterogeneidad de las especies, tan evidente para nuestros sentidos —por ejemplo, un cerdo y un gorrión—, no debe ser resultado per se de esos principios inteligibles, sino más bien, en cierta forma, accidental. Es decir: las especies sensibles no son efectos de causas orientadas per se a tales efectos, por lo que su heterogeneidad no se basa en la naturaleza esencial de las cosas y, a su vez, no debería ser impedimento para nuestras operaciones.
Por ejemplo, en vista de la ley de gravitación universal de Newton, aprendemos que no existe una diferencia esencial o heterogeneidad entre los cuerpos celestes y terrestres. De hecho, en vista de las leyes de movimiento y fuerza gravitacional de Newton, se descubre que los viajes espaciales bajo control humano son posibles, que están al alcance de nuestro poder, por lo que podemos elegir hacerlos. Al lanzar un cuerpo desde la Tierra, léase, un cohete, con la velocidad suficiente, los ingenieros pueden lograr que ascienda a los cielos y, metafóricamente, transformar un cuerpo terrestre en uno celeste. De hecho, esto se demuestra al final de los Principia de Newton. Además, por medio de etapas y maniobras orbitales basadas en la misma física, los ingenieros pueden controlar la trayectoria del cohete y hacer que se dirija hacia donde deseen. Este es un caso asombroso pero particular del conocimiento de la física y la ingeniería; no hemos dominado todos los fenómenos físicos, sino solo un tipo, los sistemas gravitacionales. Pero observemos qué ocurre con este caso particular cuando aplicamos de manera imaginaria la analogía universal de Newton: “Cualquier razonamiento concerniente a los movimientos mayores [la Tierra, el cohete, el sistema solar] también debe concernir a los menores [las partículas minúsculas de un cuerpo]” [52]. Por lo tanto, es posible imaginar que, tal como los ingenieros pueden modificar la trayectoria de un cohete en el sistema solar, en el futuro también podrían controlar las trayectorias de las partículas en un cúmulo que tradicionalmente denominamos “un gato” y transformar ese cúmulo en lo que tradicionalmente denominamos “un perro”. Hoy en día, esto puede ser difícil en un sentido práctico, a causa de la pequeñez y la enorme cantidad de partículas, pero nada hay en la naturaleza de las cosas que lo imposibilite: nada hay en su ser material y sus principios o en el proceso de percepción sensible o (como describe de Broglie) en el uso de aparatos experimentales que pueda limitar nuestro conocimiento y el control de los fenómenos. En consecuencia, como expresa asombrosamente el propio Newton, “todo cuerpo puede transformarse en otro, sin importar el tipo, y se pueden inducir en él todas las cualidades intermedias en cualquier grado” [54].

Francis Bacon
Esta es la disposición y cosmovisión paradójica e inmoderada que surge de la filosofía moderna temprana y la física clásica. Newton no está solo, no es una excepción dentro de esta perspectiva; véanse las citas 32-50 de Bacon, Descartes y Spinoza.
Nótese cómo Newton afirma explícitamente que las transformaciones que se pueden producir serán continuas: dice que “se pueden inducir en él todas las cualidades intermedias en cualquier grado”. No está claro por qué lo especifica, pero al parecer no pueden existir saltos cuánticos de una cualidad o estado a otro en los cambios que se pueden inducir en los cuerpos, como así tampoco ningún cambio sustancial.
Presenté toda esta sección bajo el título de la neutralidad específica, un nuevo tipo de relación entre lo sensible y lo inteligible. El modelo de fuerzas y partículas de Newton no solo es neutral sino también, por supuesto, reduccionista: los todos son reductibles a las partes. Cualquier principio misteriosamente holístico, como el alma aristotélica o el concepto de vida de Hegel [56], queda excluido de la naturaleza. Esta prioridad absoluta de las partes con respecto a los todos es necesaria para la tesis del transformismo universal de Newton. Cabe destacar que el darwinismo, tal como se comprende a sí mismo en la actualidad, también mantiene la neutralidad específica [65], pero no es reduccionista; no afirma que un animal no sea más que un conjunto de partes elementales y plenamente en acto. Así, para la biología darwinista, las especies evolucionan y se transmutan por variaciones aleatorias y selección natural, pero no de manera que el hombre pueda controlar manipulando las partículas de los animales. El control humano de la evolución —incluso la nuestra— es una creencia ideal de ciertos genetistas, basada en la supuesta comprensión de su capacidad para manipular el ADN [66, 67]. Pero no todos los biólogos moleculares comparten esta creencia [68, 69].
El reduccionismo neutral específico de la física clásica es tan radical que contribuye en forma directa a una de las grandes revoluciones científicas del siglo XX, la física cuántica. Los experimentos de dispersión de Rutherford en 1911 llevaron a la concepción nuclear o “planetaria” del átomo: un núcleo denso con carga positiva, rodeado de electrones en un espacio ambiental mucho mayor. A primera vista, parece un sistema solar y, por ende, una reivindicación del modelo universal de fuerzas y partículas de Newton. Pero el problema bipartito de la estabilidad de la materia se presenta ahora en los términos particulares del átomo nuclear, de la siguiente manera.
El problema de la estabilidad interna: respecto de un átomo aislado, ¿qué mantiene a los electrones negativos en su lugar alrededor del núcleo positivo (ya sea en posiciones fijas o, si los concebimos en movimiento similar al de los planetas, en órbitas de radio fijo), en razón de la fuerza eléctrica que los atrae fuertemente al núcleo? El problema de la estabilidad externa: respecto de los diversos átomos de los líquidos y los sólidos (átomos tan compactados que los materiales que componen son resistentes a la compresión), ¿qué le permite a cada átomo mantener su forma e integridad antes las fuertes perturbaciones externas (estar “apretados” contra los otros átomos) a las que se exponen permanentemente?
La teoría física clásica no puede dar respuesta a estas preguntas. La teoría clásica vuelve ininteligible la estabilidad de los átomos y, por ende, de las propiedades de las especies químicas que consisten en o se componen de átomos. Nuestra experiencia precientífica de estas propiedades es constante —por caso, la solidez de nuestros huesos y de la silla que nos sostiene— y las observamos en experimentos de laboratorio sofisticados, como el espectro cromático de la luz que emiten los gases bajo estimulación eléctrica. Este es el fracaso histórico de la física clásica y una de las puertas más conocidas a la física cuántica6.
El fracaso de la física clásica en torno al problema de la estabilidad atómica interna se describe en los manuales estándar. No existe una configuración de equilibrio estable para partículas estáticas con carga eléctrica, un teorema atribuido en su origen a Samuel Earnshaw y que se sigue directamente de la ecuación de Laplace, ∆2 Φ= 0, para el potencial eléctrico en el vacío. No existe una configuración de órbitas estable para electrones que circulan alrededor del núcleo a causa de la pérdida de energía por radiación (las cargas en aceleración generan radiación electromagnética y esto consume su energía mecánica, por lo que el electrón colapsaría en el núcleo en una fracción mínima de segundo)7.
El fracaso de la física clásica en torno al problema de la estabilidad externa lo describe Niels Bohr en pocas palabras, tal como lo reescribe Heisenberg [59]. El siguiente pasaje es en especial relevante porque ubica la dificultad en la propia noción de la trayectoria determinista de las partículas o, en un plano más general, en la evolución determinista de los sistemas, como describe de Broglie:
Mi punto de partida no fue en absoluto la idea de que un átomo es un sistema planetario a pequeña escala, regido por las leyes [similares a las] de la astronomía. Jamás lo tomé de modo tan literal. Mi punto de partida fue más bien la estabilidad de la materia, un verdadero milagro desde el punto de vista de la física clásica.
Por “estabilidad” me refiero a que las mismas sustancias siempre tienen las mismas propiedades, que los mismos cristales son recurrentes, los mismos compuestos químicos, etc. En otras palabras, aun tras una serie de cambios a causa de influencias externas, un átomo de hierro siempre seguirá siendo un átomo de hierro, con exactamente las mismas propiedades que antes. Los principios de la mecánica clásica [o el electromagnetismo clásico] no pueden explicar esto, sin dudas no si el átomo se asemeja a un sistema planetario. La naturaleza tiene una tendencia evidente a producir ciertas formas (…) y a recrear estas formas aun cuando se las perturba o destruye. Se puede pensar incluso en la biología: la estabilidad de los organismos vivos, la propagación de formas muy complicadas que, después de todo, solo pueden existir en su totalidad. Pero la biología se concentra en estructuras de alta complejidad, sujetas a transformaciones temporales y particulares que no vienen al caso. Concentrémonos en las formas más simples que estudiamos en la física y la química. La existencia de sustancias uniformes, de cuerpos sólidos, depende de la estabilidad de los átomos; esa es justamente la razón por la que un tubo electrónico que contiene cierto gas siempre emitirá luz del mismo color, un espectro con las mismas líneas. Todo esto, lejos de ser evidente, es inexplicable en términos de los principios básicos de la física newtoniana [y maxwelliana], según la cual todos los efectos tienen causas bien determinadas y el estado presente de un fenómeno o proceso está determinado en su totalidad por aquel que lo precede inmediatamente. Este hecho me resultaba muy inquietante cuando empecé a conocer la física atómica. (Heisenberg, Physics and Beyond, trad. al inglés A. J. Pomerans, 39; la cursiva es mía)
Basándonos en la teoría clásica, entonces, no hay manera en la que un estado futuro (como el estado fundamental característico de una especie determinada de átomo) pueda ser la causa de un movimiento presente8.
Podemos ver con claridad a qué se refiere Bohr si recurrimos a nuestro cálculo de la trayectoria: Imaginemos que un sistema clásico típico, el sistema solar, sufre una perturbación externa de gran magnitud. Por ejemplo, un gran cometa o asteroide pasa por el sistema solar sin entrar en colisión con ningún planeta, pero los desvía de sus órbitas previas por su propia fuerza gravitacional. ¿Existe algo en los principios fundamentales de la física newtoniana (los principios que acabamos de utilizar para calcular una trayectoria a partir de condiciones iniciales dadas) que ocasionaría que los planetas recuperen sus órbitas previas? La respuesta es no, ya que el efecto del cometa o asteroide “reinicia” las condiciones iniciales, las posiciones y las velocidades de los planetas, que entonces determinan en su totalidad las trayectorias futuras según las leyes de movimiento y fuerza (la dinámica). No hay lugar en este “tipo de razonamiento” [53] para que el sistema solar recuerde, por así decir, su configuración pasada y que retorne a ella. La neutralidad específica y el reduccionismo de la cosmovisión clásica hacen de la naturaleza algo irremediablemente informe.
Por lo tanto, no resulta sorprendente que el tipo de teoría necesaria para los fenómenos de la estabilidad atómica y molecular no posea estas tres características fundamentales de toda la física clásica: (1) continuidad del espacio, el tiempo y el movimiento, (2) representabilidad en principio de los procesos elementales y (3) causalidad determinista. En particular, no resulta sorprendente que la “trayectoria de partículas” y la “magnitud de campo”, los conceptos centrales de la física clásica, pruebe ser falsa en la naturaleza a escala atómica.

Werner Heisenberg
“Secularismo” fisicomatemático: en torno a la cuestión de la diferencia entre los objetos matemáticos y los objetos físicos
¿Hay alguna diferencia fundamental entre los objetos matemáticos y los objetos físicos? Platón dice que sí. Aristóteles dice que sí, pero no como cree Platón. Descartes dice que no; el objeto de la física, la materia en movimiento, es el objeto de la geometría. Newton dice que debemos dejar de lado este problema filosófico y asumir que cualquier diferencia entre lo matemático y lo físico no concierne a la implementación de nuestra física matemática. De allí en más, cada cual puede tener sus creencias personales sobre los modos de ser de los objetos matemáticos y físicos, tal como las fuerzas centrales, pero esta pregunta no reviste ningún interés científico. (La analogía con el secularismo en la teoría política moderna temprana es clara: las creencias religiosas serán un asunto privado; las diferencias entre católicos y protestantes, por ejemplo, no han de afectar al ejercicio del gobierno).
De más está decir que, como los objetos matemáticos no están sujetos per se al movimiento, que es la actualización de una potencia [7], el secularismo fisicomatemático conlleva desterrar de la física la noción aristotélica fundamental de la potencialidad y los grados de ser en función del acto y la potencia.
El secularismo fisicomatemático se basa en el uso de coordenadas cartesianas y magnitudes para representar el espacio y el tiempo físicos y las propiedades físicas de los cuerpos, las partículas y los campos, como describe de Broglie. Consideremos la trayectoria de la partícula antes calculada y representada en papel: En cada instante de tiempo, t, la partícula posee un valor de posición con precisión numérica real, x, y, z, y un valor de momento con precisión numérica real, mvx, mvy, mvz, así como energía, E. En general, suponemos que estas magnitudes variables pueden representar con fidelidad cualquier cosa medible en el mundo físico. Suponemos, entonces, que los objetos físicos tienen propiedades con valores de precisión numérica real. Se presume luego que nuestras mediciones y cálculos revelan, predicen y por último controlan las cantidades físicas de existencia objetiva en el espacio y el tiempo. ¿No será que confundimos los objetos matemáticos con los objetos físicos? No hay problema, eso no concierne a nuestra materia (el doble sentido es deliberado): la reificación inadvertida de los objetos matemáticos no afecta a la física; esto se sigue de haber dado por sentado en principio el secularismo fisicomatemático.
Esta presunción, establecida en el siglo XVII, es cuestionable, más que nada en vista del carácter sumamente artificial de las magnitudes numéricas cartesianas que se utilizan en nuestra física. Para aclarar qué quiero decir con “carácter sumamente artificial”, observemos las dos magnitudes que se muestran en negrita.

¿Estas magnitudes son iguales o desiguales? La respuesta es sí. Como magnitudes euclidianas de primera intención, por supuesto que son desiguales, ya que puedo colocar una al lado de la otra, cortar una parte de la magnitud derecha que sea igual a la magnitud izquierda y observar lo que resta. Pero como magnitudes cartesianas simbólicas, que en nuestras mentes poseen un valor numérico, punto por punto, según nuestra elección de una unidad de medida, por supuesto que son iguales, ya que ambas tienen el mismo valor numérico real, c9. A diferencia de los matemáticos premodernos, nosotros contamos con dos conceptos de magnitud distintos en nuestra caja de herramientas mental. La magnitud cartesiana es un artefacto o constructo mental muy sofisticado. La idea de que el espacio y el tiempo físicos, así como los entes físicos genuinos, se pueden sustituir mentalmente por las magnitudes cartesianas sin afectar a nuestro conocimiento de la naturaleza es muy discutible.
Por ejemplo, el secularismo fisicomatemático deja a la física clásica sin respuesta ante algo como el principio de incertidumbre de Heisenberg, es decir, ∆x∆p ≥ h/2Π, ∆E∆t ≥ h/2 Π. Este principio significa, entre otras cosas, que el ser y la cognoscibilidad de las propiedades espaciotemporales, como la posición de una partícula, x, en un tiempo, t, están interrelacionadas con el ser y la cognoscibilidad de las propiedades dinámicas, como el momento, p, y la energía, E. Una vez más, Louis de Broglie [62]:
Lo que ahora es particularmente importante que comprendamos es el significado profundo de esta idea misteriosa del cuanto de la acción [la constante de Planck, h = 6.62×10-27 ergio-seg]. Hasta [principios del siglo XX] el espacio y el tiempo de la física clásica, o de su sucesor (el espacio-tiempo de la física de la relatividad), se nos mostraban como un marco dado a priori, bastante independiente de lo que uno insertara allí, bastante independiente en particular de los movimientos y la evolución de los cuerpos que se ubicaran allí (…).
La verdadera relevancia del cuanto de la acción [la constante de Planck, h] nos fue dada a conocer, en especial, gracias al descubrimiento de las incertidumbres de Heisenberg. (…) Hoy parece innegable que la existencia del cuanto de la acción expresa una unión nunca antes sospechada entre el marco del espacio y el tiempo y los fenómenos dinámicos que ocurren en él. La imagen del espacio y el tiempo [en la física clásica] es en esencia estática; un cuerpo, un ente físico, que posee una ubicación exacta en el tiempo y el espacio carece, por este mismo hecho, de toda propiedad evolutiva; por el contrario, un cuerpo que se desarrolla, dotado de propiedades dinámicas, no puede permanecer, en realidad, sujeto a ningún punto del espacio y el tiempo. Estas son de consideraciones filosóficas que se remontan a Zenón [y, entonces, a Aristóteles] (…). Las relaciones de incertidumbre de Heisenberg parecen estar en consonancia con estas afirmaciones; nos enseñan, en efecto, que es imposible atribuir simultáneamente a un cuerpo un movimiento bien definido y un lugar bien determinado en el espacio y el tiempo. (Physics and Microphysics, 120-22)
En la concepción clásica de la mente y el mundo, del espacio y el tiempo, de la matemática y la física, de la medición y el cálculo, no hay manera de que nuestro conocimiento de cierta cantidad física, como la posición o el tiempo, pudiera afectar, interferir o limitar nuestro conocimiento de otra cantidad, como el momento o la energía. No son más que magnitudes cartesianas. Pero, como nos recuerda de Broglie, remontándose a Aristóteles, un cuerpo en movimiento —en oposición a un punto matemático que se “mueve” en nuestra imaginación— no se encuentra en realidad en un lugar o posición fija; si así fuera, no estaría en movimiento. Aristóteles, por supuesto, no cuantificó la indeterminación de la posición de un cuerpo en movimiento a cierta velocidad: no descubrió la constante de Planck. Pero Aristóteles sí nos prepara para la idea de la indeterminación (de que algunas cosas tengan menos ser que otras) y, por ende, de los límites de la inteligibilidad del ser potencial.
Albert Einstein
Conclusión
Por otra parte, la física cuántica revela algo inesperado para cualquier antecesor de Einstein y su famoso debate con Bohr, entre 1927 y 1935. Esto nuevo es la no localidad o entrelazamiento, las correlaciones Einstein-Podolsky-Rosen (EPR) que Einstein denominó “acción fantasmal a distancia”10. Esta es la metáfora que utilizó Einstein para ilustrar el efecto y expresar su sentimiento de frustración y rechazo a la física cuántica.
Imaginemos una pelota en una de dos cajas. Cada caja tiene una tapa con bisagra que se puede abrir para observar si la pelota está allí o no. Ocurre que no sabemos en qué caja está la pelota. Podemos caracterizar el estado de nuestro conocimiento si decimos que hay un 50 % de probabilidades de que la pelota esté en una u otra caja. Luego, abrimos una de ellas y así descubrimos dónde estaba la pelota. Al descubrir en qué caja estaba, nuestra ignorancia se reduce a una certeza. Sería absurdo pensar que nuestro acto de observación creó la presencia o ausencia de la pelota en la caja que abrimos. Pero esto es lo que dice la interpretación de Copenhague de la física cuántica. La probabilidad del 50 % no era solo una característica de nuestro conocimiento, sino también (de alguna manera) del ser de la pelota. Muy bien, dice Einstein, ¿cuánto tarda, por ejemplo, la información de que la caja 1 está vacía (ya que observamos qué hay dentro) en propagarse por el espacio a la caja 2, donde entonces se produce la pelota? La interpretación de Copenhague dice que nada, es instantáneo. Einstein hace luego su última pregunta: ¿qué tan lejos pueden estar las dos cajas? Y la respuesta es: la lejanía es arbitraria, la física cuántica no limita la separación espacial de las cajas. Para Einstein, el creyente comprometido con la física clásica, la naturaleza sencillamente no puede ser así.
La metáfora de la pelota y las cajas es, desde ya, una analogía, y toda analogía es imperfecta. Las cajas y los estados de las cajas (ocupada, no ocupada) representan pares de fotones o partículas en estados de polarización (vertical, horizontal) o espín (arriba, abajo). A diferencia de las cajas, solo se puede acceder a estos sistemas cuánticos a través de experimentos en varias etapas que requieren de un ingenio extraordinario para preparar los fotones o partículas en estados pares con la propiedad cuántica de la coherencia. Según recuerdo, se han observado en laboratorio correlaciones EPR a distancias de entre 6 y 12 metros, a partir de los experimentos de Aspect en 198211. La gran pregunta es: ¿qué comprensión filosófica sería adecuada para este fenómeno tan inusual?

Richard F. Hassing
NOTAS
1 Bacon, New Organon 11.52; ver también I 88,1.129, II 1-6, y Wisdom of the Ancients XIII, sobre Proteo. En The Advancement of Learning, Bacon se refiere a “la dignidad y excelencia del conocimiento y el aprendizaje sobre aquello que es la mayor aspiración de la naturaleza del hombre, esto es, la inmortalidad o persistencia” (The Works of Francis Bacon, ed. Spedding, Ellis y Heath, vol. III, p. 318). Ver también Descartes, Discurso del método, parte 6, AT VI 61-62, CSM I 142-43 y Principios (francés) III.44, AT IXB 155, CSM I 255.
2 Stanley Shostak, Becoming Immortal. Combining Cloning and Stem-Cell Therapy (Albany: SUNY Press, 2002).
3 Me refiero a algo más sutil (pensemos en las citas 1-5) que la tendencia común a concluir la inmoralidad a partir de la física por medio de analogías pobres. Estos son un par de ejemplos excelentes a partir de la física del siglo pasado: “Einstein demostró que todos los valores son relativos al sistema de referencia y que no existe un sistema absoluto. Por lo tanto, nada está mal en sentido absoluto y entonces puedo hacer lo que quiera”.
4 Tan solo para empezar: ¿es el órgano de percepción externo al sujeto que percibe?
5 Tomo la frase “neutralidad específica” [species-neutrality] de Richard Kennington, un extraordinario profesor de filosofía moderna temprana. El término “secularismo” lo tomo de Francois De Grandt: “Newton optó por tratar las fuerzas de manera puramente matemática; por omisión inicial —que en cierto sentido llegó a ser definitiva—, dejó en suspenso las preguntas de carácter filosófico o físico sobre las causas de la gravitación y la realidad ontológica de la fuerza. Esta neutralidad (o “secularismo”) de la fuerza centrípeta frente a las controversias sobre la causa de la gravitación es la característica esencial de la nueva ciencia”. Force and Geometry in Newton’s Principia, trad. Curtis Wilson (Princeton University Press, 1995), x-xi.
6 Durante unos dos siglos, la física clásica resolvió todo tipo de problemas de ingeniería dando por sentadas las propiedades estables de los líquidos y los sólidos se daban por sentado e incorporándolas a ecuaciones como condiciones de frontera o constantes determinadas empíricamente. Por ejemplo, el agua es incompresible y tiene una viscosidad dada, mientras que el cemento es sólido, a diferencia de la manteca, y contiene al agua en una piscina cuya superficie será horizontal, estando en equilibrio dentro del campo gravitacional de la Tierra. Al ser perturbada, el agua propagará ondas superficiales y volverá luego a su estado de equilibrio estable con una superficie plana. Esto no explica, sin embargo, las respectivas características del agua y el concreto en términos de sus constituyentes atómicos y moleculares o de los núcleos y electrones. Para ello, hace falta la física cuántica.
7 Véase William Thomson y P. G. Tait, Treatise on Natural Philosophy (Oxford: Clarendon Press, 1857), 372-73; L. D. Landau y E. M. Lifshitz, The Classical Theory of Fields (Reading, MA: Addison-Wesley, 1962), 100; R. M. Eisberg, Fundamentals of Modern Physics (Nueva York: John Wiley & Sons, 1961), 108- 109, también 366-69 sobre la gran importancia del principio de exclusión de Pauli.
8 Esta es una formulación imprecisa pero didáctica de la causalidad final.
9 Jacob Klein, Greek Mathematics and the Origin of Algebra (Cambridge, MA: M.I.T. Press, 1968), 117-25, 197-211.
10 Einstein a Max Born (1947) en Max Born, The Born-Einstein Letters (Nueva York: Walker and Co., 1971), 158.
11 Ver Tim Maudlin, Quantum Non-Locality and Relativity (Malden, MA: Blackwell, 2002).
Citas de la historia de la filosofía y la ciencia
Richard F. Hassing, TAC, 7 de marzo, 2003
Revisión: 18 de junio, 2008
Ética aristotélica: deseo, capacidad, elección, disposición, apariencia.
[1] [La elección] no es un deseo, a pesar de su manifiesta proximidad; pues no hay elección de lo imposible (…) mientras que el deseo puede ser de cosas imposibles, por ejemplo, de la inmortalidad. (…) Pero nadie elige estas cosas, sino las que uno cree poder realizar por sí mismo. (…) La elección, en general, parece referirse a cosas que dependen de nosotros. (EN2, 111l b20-30)
[2] “Bueno” y “malo” significan una cualidad sobre todo en los seres que poseen un alma [animados] y, de estos, sobre todo los que tienen albedrío. (Meta. 5.14, 1020b23-25)
[3] El origen de la acción (…) es la elección, y el de la elección es el deseo y el razonamiento con miras a un fin. Es por ello que la elección no puede existir sin intelecto o razón ni sin una disposición ética, en tanto que la buena acción y su opuesto no pueden existir sin una combinación de pensamiento y carácter. (EN 6.2, 1139a31 -35)
[4] Cada estado de carácter tiene sus propias ideas sobre lo noble y lo placentero. (AE3.4, 1113a.32)
[5] Todo deseo (orexis) (…) ocurre por el objeto de deseo (orekton), que es el punto de partida del intelecto práctico. (…) El intelecto no parece ser causa del movimiento sin deseo (orexis); la volición (boulésis) es una especie de deseo (orexis), y cuando un hombre se mueve según el razonamiento, también se mueve según la volición (boulésis) [véase EN3, 1113a11-13]. Pero el deseo (orexis) [también] puede ser causa de movimiento en contra de la razón; ya que el apetito (epithumia) es un[a] [especie de] deseo (orexis). El intelecto acierta en todos los casos; pero el deseo (orexis) o la imaginación [pueden] acertar o no. En vista de estos hechos, aquello que ocasiona el movimiento siempre es el objeto de deseo (orekton); pero este objeto puede ser el bien o el bien aparente (…). (De Anima 3.10, 433a16-29)
[6] “Quien ignora (dice el proverbio) no recibe las palabras del conocimiento, a menos que antes se le diga aquello que guarda en su propio corazón”. (Bacon, “The Plan of the Great Instauration”, párr. 2)
Física aristotélica: todos y partes, acto y potencia.
(Los todos son mayores que las partes; las partes pueden estar en potencia en el todo; el movimiento es acto solo en parte).
[7] El movimiento es la actualidad de lo potencial como tal. (…) Se cree que el movimiento es cierto tipo de actualidad, mas es incompleto; y la causa de ello es que el potencial, de lo que esto es el acto, es incompleto…. El movimiento es (…) difícil de aprehender, pero capaz de existir (…). (Física 3.1, 201a11, 3.2, 201b32-33, 202a2)
[8] Nada que esté en movimiento puede ser [indivisible] en un momento. (…) Todo lo que cambia es por necesidad divisible. (Física 3, 234a25, 6.4, 234b10)
[9] Y se dice que lo que es continuo y limitado es un todo cuando es una cosa compuesta de diversos constituyentes, en especial cuando estos existen en potencia (…). (Meta. N26, 1023b33-34)
[10] [Las partes materiales] no pueden existir separadas del todo; en tanto que el dedo de un animal no lo es de cualquier manera, dado que se le llama “dedo” por equívoco una vez muerto. (Meta. VII.10, 1035b23-25)
[11] En tanto que una mano es parte del cuerpo no de cualquier manera, sino solo cuando puede realizar su función, [el animal] debe estar vivo; si no, no es una parte. (Meta. VII. 11, 1036b31-32)
[12] El todo debe ser superior a la parte por necesidad; porque si se destruye el todo [cuerpo], ya no habrá un pie o una mano, excepto en el sentido de que el término sea similar (como cuando se habla de una mano de piedra), pero la cosa en sí será defectuosa (…). (Pol.I.2, 1253al9-24)
[13] Cuando el animal es uno y continuo por naturaleza (…) toda parte existe en potencia. (Meta. VII. 16, 1040b 15-16)
[14] Si el ojo fuera un animal, la visión sería su alma, (…) y al cesar la visión, ya no existe un ojo, excepto por equívoco, como ocurre con el ojo de una estatua o pintura. (…) Tal como el ojo es su visión con la pupila, así el animal es su alma con el cuerpo. (De An. II.1, 412bl9-22, 413a3)
[15] Si el alma se hallara en una sola parte como una forma, no sería el acto de un cuerpo orgánico, sino el acto de un solo órgano, por ejemplo, del corazón o de otro órgano similar; y las demás partes del cuerpo recibirían su acto de otras formas. Por lo tanto, el cuerpo entero no sería una unidad natural, sino una mera conjunción de partes [las partes no estarían en potencia en el todo, sino en acto, como en un artefacto]. Entonces, se sigue que existe una sola alma en todo el cuerpo y cada una de sus partes. (Santo Tomás de Aquino, Cuestiones sobre el alma, c 10)
Física aristotélica: relación entre lo sensible y lo inteligible.
(Es específica, lo que tienen en común las diferentes especies naturales no es tan fundamental como lo que las diferencia y especifica).
[16] ¿Deberíamos (…) comenzar por tratar cada especie por separado (hombre, león, buey, entre otros), considerando a cada especie por separado del resto, o más bien deberíamos tratar primero los atributos que tienen en común, en virtud de cierto elemento común en sus naturalezas (…)? Queda claro que si tratamos sobre cada especie por separado del resto, con frecuencia nos veremos obligados a repetir lo mismo una y otra vez (…). Las causas que conciernen a la generación de las obras de la naturaleza son, como es manifiesto, múltiples. Existe la causa final y la causa eficiente. Resta decidir cuál de estas dos causas es la primera, cuál la segunda. Es claro, sin embargo, que la causa primera es aquella que llamamos final. (Partes de los animales, 639al5-25, bl2-l 5)
[17] Los principios y los elementos no pueden ser los mismos para todas las cosas, excepto por analogía, es decir, en el sentido en el que se podría decir que existen tres principios: la forma, la privación y la materia; pero cada uno de estos es distinto para cada género. (Meta. 1070b 18-20)
[18] La materia es una de las cosas relativas: a una forma diferente corresponde una materia diferente. (Fís. 194b9)
[19] Todas las cosas que cambian tienen materia, pero a las cosas distintas corresponde materia distinta. (Meta. 1069b25)
[20] En cada movimiento, es el sujeto pasible de tal movimiento quien lo experimenta. (Fís. 25la14)
[21] El alma no es un cuerpo, sino algo de un cuerpo y, a causa de ello, existe en un cuerpo. Pero existe en tal o cual cuerpo y no como creían los antiguos pensadores; ellos la atribuían a un cuerpo sin especificar de qué cuerpo se trataba o qué tipo de cuerpo era, aunque no existe evidencia de que cualquier cuerpo aleatorio pueda recibir cualquier alma aleatoria. También, según la razón, ocurre que la actualidad de cada cosa [solo] puede existir, por su naturaleza, con la potencialidad que le pertenece a aquella cosa o con su materia apropiada. (De An.2, 414a20-28)
[22] Lo que cada cosa es (por ejemplo, un ser humano, un caballo o un hogar) cuando llega a la plenitud de su ser (tés geneseós telestheisés) es, decimos, la naturaleza de esa cosa. (Pol. 1252b32-34)
[23] Lo mejor es aquello por lo que se es, el fin. (Pol. 1253al)
[24] Lo que por naturaleza es propio a cada cosa será al mismo tiempo lo mejor y lo más placentero para ella. (Ética Nic. 1178a5)
[25] ¿Cuál puede ser entonces esta función (ergon) [humana]? La mera vida parece ser lo común a las plantas, mientras que buscamos aquello que es distintivo [del ser humano]. (Ética Nic. 1097b33-1098al)
[26] La naturaleza no hace nada en vano (…) el hombre es el único entre los animales que posee habla. (Pol. 1253a8-9)
[27] Lo peculiar al hombre, en comparación con los demás animales, es que es el único que tiene una percepción de lo bueno y lo malo, lo justo y lo injusto. (Pol. 1253al 5-17)
[28] El alma y las demás formas naturales no están per se sujetas al movimiento (…) son, además, las perfecciones de las cosas mutables. (Santo Tomás de Aquino, In de trinitate, c. 5, r. 2, ad 6)
Física aristotélica: la forma como origen y límite del conocimiento.
[29] El límite significa (…) la sustancia de cada cosa o la esencia (to ti en einai) de cada cosa, ya que se dice que es el límite del conocimiento y, si lo es del conocimiento, también lo será de la cosa. (Meta. V. 17, 1022a5, 9-10)
[30] La esencia no corresponderá a nada que no sea una especie (eidos) de un género, pero solo a una especie de un género. (…) Por forma (eidos) quiero significar la esencia de cada cosa. (Meta. VII.4, 1030al2-13, VII.7, 1032b2)
Filosofía moderna temprana y física clásica: relación entre lo sensible y lo inteligible, reduccionismo, transformismo.
(La relación entre lo sensible y lo inteligible es de neutralidad específica, lo que los tipos naturales tienen en común es más fundamental que lo que los diferencia específicamente).
Un precursor antiguo:
[31] Estrepsíades: ¿Conoces la casa de al lado?
Fidípides: Sí. ¿Qué es?
Estrepsíades: Ese, hijo mío, es el Pensadero. Se dice que es solo para las mentes brillantes. Es donde viven los científicos, los que intentan probar que el cielo es como uno de esos objetos redondos para hornear pan. Dicen que nos rodea y que…
Fidípides: Y que somos los carbones, ¿verdad?
Estrepsíades: Así es, comprendes bien.
(Aristófanes, Las nubes, 92-96)
Bacon:
[32] Cuando el hombre contempla el libre obrar de la naturaleza, reconoce diferentes especies de cosas, de animales, de plantas, de minerales; esto lo lleva sin más a creer que en la naturaleza existen ciertas formas primarias que esta se esfuerza por educir. (New Organon,66)
[33] En realidad, nada existe en la naturaleza más allá de los cuerpos individuales [verdaderas partículas, II.8, es decir, no hay formas], que realizan actos puramente individuales [por ende, no existen partes potenciales en el todo] según leyes. (New Organon, II.2)
[34] Las formas son creaciones de la mente humana, a menos que se llame formas a esas leyes de acción. (New Organon, 1.51)
[35] La filosofía en boga por estos días acepta y sostiene ciertos principios (…) con respecto a la doctrina de que el calor del Sol y del fuego difieren en su especie [porque los cuerpos celestes y los terrestres son distintos en esencia; 198a30-32] (…). Estos conceptos, tomados en serio, tienden en su totalidad a la injusta limitación de la capacidad humana (…). Por el contrario, resulta poco fructífero investigar la naturaleza de algo [como el calor o la gravitación] en la cosa misma [fuego, una piedra], siendo que la misma naturaleza [el calor; la gravitación] que en algunas cosas parece estar [aqua vitae; movimientos celestes] latente y oculta, en otras [fuego; una piedra], es manifiesta y palpable (…). (New Org.,88)
[36] La obra y el fin de la capacidad humana es generar e inducir una o varias naturalezas nuevas en un cuerpo determinado (…). (New Org., 1)
[37] El hombre que conoce la causa de cualquier naturaleza (como la blancura o el calor) solo en ciertos sujetos tiene un conocimiento imperfecto (…). Pero quien conozca [las leyes de la naturaleza] aprehende la unidad natural en materiales muy distintos [por ejemplo, un imán y el cuerpo humano] y es capaz, por tanto, de detectar y producir cosas jamás logradas [imagen por resonancia magnética en el diagnóstico médico], tal que ni las vicisitudes de la naturaleza, ni la destreza experimental, ni el azar mismo, podrían haber llevado a cabo (…). (New Org., II.3)
[38] Se dice (…) que existen tres tipos de calor: el calor de los cuerpos celestes, el calor de los animales y el calor del fuego; y que estos calores (…) son en su misma esencia y especie (es decir, en su naturaleza específica) distintos y heterogéneos (…). Pero la comprensión [baconiana], que rechaza la noción de heterogeneidad esencial, se presta fácilmente [gracias al Método] a indagar cuáles son en realidad [en oposición a nuestras opiniones erróneas sobre la forma] aquellas diferencias entre el calor del Sol y el del fuego (…) aunque compartan una naturaleza [baconiana] común. (New Org., 11.35)
Descartes:
[39] Son escasas las naturalezas puras y simples que podemos intuir, ya sea por nuestra experiencia o por algún conocimiento innato en nosotros, como primarias y per se (…). La figura, la extensión, el movimiento, etc., son algunos casos (…). Basta tener aunque sea una mínima aprehensión de [una naturaleza simple, por ejemplo, de una recta] (…), [entonces] la conocemos por completo. (Regulae, VI, XII)
[40] Por “naturaleza” no quiero decir aquí cierta diosa o algún otro tipo de poder imaginario. Más bien, utilizo ese término para significar la materia misma (…). (Le Monde, Cap. 7)
[41] Asumo que la cantidad de la materia que describí no difiere de su sustancia (…) [y] concibo su extensión (…) no como un accidente, sino como su verdadera forma y su esencia. (Le Monde, Cap. 6)
[42] La naturaleza del cuerpo no consiste en su peso, dureza, color y demás, sino sencillamente en la extensión. (Principios, 4)
[43] Comprendemos que esta naturaleza [de extensión o sustancia corpórea] es exactamente la misma en cualquier parte del espacio que en la totalidad de este. (Principios, 8)
[44] Toda la variedad en la materia, toda la diversidad en sus formas, depende del movimiento [local de retazos de extensión]. (Principios, 23)
[45] Los únicos principios que acepto o exijo en la física son los de la geometría y la matemática pura; estos principios explican todos los fenómenos naturales (…). (Principios, 11.64)
[46] Fue muy difícil para mí describir todo lo que concierne a la naturaleza del fuego de manera muy clara y comprensible… Así, expuse cómo se forma y se alimenta, cómo a veces solo posee calor sin luz, otras veces luz sin calor; cómo puede producir diferentes colores y muchas otras cualidades en diversos cuerpos; cómo derrite algunos cuerpos y endurece otros; cómo puede consumir casi todos los cuerpos o convertirlos en ceniza y humo; por último, cómo puede, por su solo accionar violento, formar vidrio a partir de estas cenizas, algo que me resultó particularmente placentero de describir, ya que me parece una transmutación tan asombrosa como cualquiera de las que ocurre en la naturaleza. (Discurso del método, Parte V, AT VI44-45)
[47] Las naturalezas [de todas las cosas puramente materiales, incluyendo los animales] son mucho más sencillas de concebir si las vemos desarrollarse de esta manera, poco a poco (peu a peu), que si las consideramos solo como algo hecho por completo (toutes faites). (Discurso del método, Parte V, AT VI 45)
[48] Solo la voluntad, o el libre albedrío, que experimento en mí es de una magnitud tal que la idea de cualquier facultad superior sobrepasa mi entendimiento; tanto es así que, por encima de todo, es en virtud de la voluntad que entiendo que soy, de alguna manera, imagen y semejanza de Dios. (Cuarta meditación, AT VII 57)
Spinoza:
[49] Aquello que es común a todos [los cuerpos] (…) y que está por igual en una parte y en el todo [por ejemplo, la extensión cartesiana, la masa newtoniana] no constituye la esencia [la forma natural aristotélica; 1030al2] de ninguna cosa particular (…). Aquellas cosas que son comunes a todos (…) no pueden concebirse si no es adecuadamente. (Ética, 11.37, 38)
[50] Nada ocurre en la naturaleza que pueda considerarse una falla en ella [cf. Fís. 199b4]; porque la naturaleza es siempre la misma y en todas partes una y la misma en su eficacia y capacidad de acción; es decir, sus leyes y órdenes, por las que todas las cosas son y cambian de una forma a otra, son iguales en todo lugar y momento; tal que debe haber una sola y única comprensión de la naturaleza de todas las cosas en absoluto, es decir, a través de las leyes y normas universales de la naturaleza. (Ética, III, Introducción)
Newton:
[51] Existe un poder de gravedad que afecta a todos los cuerpos, proporcional a las diversas cantidades de materia que contienen (…) [e] inversamente proporcional al cuadrado de la distancia (…) [F = -GMm/R2]. (Principia, III, Prop. 7 y Cor. 2)
[52] La Naturaleza es sumamente simple y consistente consigo misma. Cualquier razonamiento concerniente a los movimientos mayores [por ejemplo, del sistema solar] también debe concernir a los menores [de los átomos]. (“Unpublished Conclusion of the Principia”, en A. R. y M. B. Hall, Unpublished Scientific Papers of Isaac Newton, 333)
[53] A partir de los fenómenos celestiales, obtengo las fuerzas de gravedad por las que los cuerpos tienden al Sol y a los diversos planetas. Luego, a partir de estas fuerzas (…), deduzco los movimientos de los planetas, los cometas, la Luna y el mar. Mi deseo es conocer el resto de los fenómenos de la Naturaleza a través del mismo tipo de razonamiento basado en principios mecánicos, en tanto que muchas razones me llevan a sospechar que todos ellos podrían depender de ciertas fuerzas por las que las partículas de los cuerpos, por causas hasta ahora desconocidas, se impelen mutuamente la una contra la otra y convergen (…), o bien se repulsan y retroceden (…). Al ignorar estas fuerzas, hasta ahora los filósofos han intentado en vano investigar la Naturaleza. (Principia, 1686, Prefacio)
[54] Todo cuerpo puede transformarse en otro, sin importar el tipo, y se pueden inducir en él todas las cualidades intermedias en cualquier grado. (Principia, primera edición, Hipótesis III)
Leibniz:
[55] Creo que las mónadas tienen existencia plena y que no podemos concebir que las partes se hallen en potencia en el todo. (Leibniz, carta a Des Bosses, 16 de junio, 1712)
Hegel (un holista posnewtoniano):
[56] La noción del todo es contener partes: pero si se toma el todo y se hace de él lo que su noción expresa, es decir, si se lo divide, deja al punto de ser un todo. No hay duda de que existen cosas que responden a esta relación: pero, por esa misma razón, son existencias inferiores. (…) La relación del todo y las partes resulta sencilla de aprehender para el entendimiento reflexivo, y por eso mismo suele ser suficiente cuando la cuestión gira en realidad en torno a temas más profundos. Los miembros y órganos de un cuerpo orgánico, por ejemplo, no son sus meras partes: solo en su unidad son lo que son, y no cabe duda de que se ven afectados por dicha unidad, a la que a su vez afectan. Estos miembros y órganos se convierten en [meras] partes solo en manos del anatomista, cuya ocupación, cabe recordar, no es el cuerpo vivo, sino el cadáver. No es que tal análisis sea ilegítimo: solo quiero decir que la relación externa y mecánica del todo y las partes no es suficiente para nosotros si pretendemos estudiar la vida orgánica en su verdad. (Hegel, Encyclopedia Logic, sec. 135, nota; ver también sec. 38, nota)
Helmholtz:
[57] Los fenómenos naturales deben relacionarse con los movimientos de una materia que posea fuerzas motrices invariables, fuerzas que solo dependan de relaciones espaciales. (…) Sin embargo, la fuerza que dos masas enteras ejercen entre sí debe resolverse en las fuerzas de todas sus partes entre sí; por tanto, la mecánica se refiere a las fuerzas de puntos materiales, es decir, a los puntos espaciales ocupados por materia. (…) Por último, la tarea de las ciencias naturales físicas debe ser la siguiente: reducir los fenómenos naturales a fuerzas de atracción y repulsión invariables cuya magnitud dependa de la distancia. La factibilidad de esta tarea es, al mismo tiempo, condición para una plena comprensibilidad de la naturaleza. (“On the Conservation of Force”, Wissenschaftliche Abhandlungen, Vol. I, pp. 15-16)
De Broglie: la concepción del mundo según la física clásica
[58] Con las coordenadas [cartesianas] de espacio y tiempo, la física matemática clásica estaba en condiciones de representar de manera precisa la sucesión de fenómenos que nuestros sentidos nos permiten verificar a nuestro alrededor.
Desde ese momento, apareció con mucha naturalidad un camino ante a la física teórica, por el que transitó audaz. Se pensaba que toda evolución del mundo físico debía estar representada por cantidades [por ejemplo, la posición y el momento de una partícula] localizadas en el espacio y variables a lo largo del tiempo. Estas cantidades debían posibilitar la descripción completa del estado del mundo físico a cada instante y, por lo tanto, la descripción de toda la naturaleza por medio de cifras y movimientos, según el programa de Descartes. Esta descripción se llevaría a cabo en su totalidad con la ayuda de ecuaciones diferenciales (…) que nos permitieran seguir la ubicación y la evolución a lo largo del tiempo de todas las cantidades que definen el estado del mundo físico. ¡Una concepción magnífica por su simplicidad y confirmada por los éxitos que obtuvo durante tanto tiempo! Sostuvo y orientó todos los esfuerzos de las grandes corrientes de física matemática del siglo XIX.
Sin dudas, no todos los científicos adherían de la misma manera a esta descripción del mundo por medio de cifras y movimientos. Algunos con una imaginación vivaz y concreta buscaron representar los elementos del mundo material de manera que los fenómenos que observan nuestros sentidos surgieran de la existencia y el movimiento de átomos o corpúsculos demasiado pequeños para ser observados directamente; pretendían desmantelar toda la máquina para ver todos los engranajes en funcionamiento. Otros, más cautos y, sobre todo, dotados de una mente más abstracta, pretendían contentarse con solo representar los fenómenos por medio de cantidades directamente medibles y desconfiaban de las hipótesis (a sus ojos, demasiado especulativas e inútiles) de los atomistas. Y si bien los atomistas avanzaban con intrepidez, abrían nuevos caminos y permitían que la ciencia gozara de un progreso asombroso, los energistas, impedidos por sus métodos más formales y cautos, retenían cierta ventaja desde el punto de vista conceptual cuando criticaban los aspectos más simplistas e ingenuos de las representaciones que proponían sus audaces rivales. Pero, sin ser conscientes de ello, ambos [los atomistas y los energistas] aceptaban ciertos (…) postulados comunes que el futuro habría de probar endebles.
De hecho, estaban de acuerdo en admitir la validez de la estructura abstracta del espacio y el tiempo, la posibilidad de seguir la evolución del mundo físico gracias a cantidades ubicadas con precisión en el espacio que variaran continuamente a lo largo del tiempo y la legitimidad de describir todos los fenómenos por medio de grupos de ecuaciones diferenciales. Aunque los energistas, como Pierre Duhem, se negaban a admitir la intervención ubicua de un “movimiento local” que se pudiera representar a través de un desplazamiento de partes, afirmaban sin más la consideración de “movimientos generales” definidos de manera más abstracta por las variaciones de cantidades a lo largo del tiempo. A pesar de sus diferencias de opinión sobre cómo implementar este programa, todos los teóricos estaban de acuerdo, entonces, en representar el universo físico con cantidades bien definidas en espacio y tiempo y sujetas a ecuaciones diferenciales.
Las ecuaciones diferenciales (…) de la física matemática clásica tienen el carácter común de permitirnos seguir rigurosamente toda la evolución de los fenómenos que describen, si suponemos la existencia de ciertos datos conocidos relativos a un estado inicial que se corresponda con un valor de tiempo particular. De allí se dedujo la posibilidad de establecer una cierta interconexión inevitable de todos los fenómenos y se llegó, por lo tanto, a la concepción de un determinismo universal de los fenómenos físicos. No me propongo evaluar la idea del determinismo universal desde el punto de vista filosófico ni necesito preguntarme a mí mismo, por ejemplo, si la mente, que al fin y al cabo es la creadora de la física matemática, podría recuperar su lugar en una naturaleza concebida de manera tan rígida. Lo cierto es que los fenómenos físicos, tal como se los representaba con exactitud por medio de las ecuaciones diferenciales de la física clásica, estaban sujetos a un determinismo definido de manera sumamente precisa.
La física clásica representaba así la totalidad del universo físico tal como se lo proyectaba con precisión absoluta en el marco del espacio y el tiempo, a partir del que evolucionaba de acuerdo con las leyes de necesidad inexorable. Hacía a un lado por completo los medios utilizados para obtener un conocimiento de las distintas partes de este vasto mecanismo, ya que, si bien reconocía la existencia de errores experimentales, solo veía en ellos el resultado de una falta de precisión en nuestros sentidos y de la imperfección de nuestras técnicas [experimentales], y aceptaba la posibilidad de reducirlos indefinidamente, al menos en principio, gracias al perfeccionamiento adecuado de nuestros métodos. Todas estas representaciones se basaban, en esencia, en las ideas clásicas del espacio y el tiempo; durante mucho tiempo parecieron bastar para describir la evolución del mundo material. (Physics and Microphysics, 116-18)
Física cuántica:
[59] Mi punto de partida no fue en absoluto la idea de que un átomo es un sistema planetario a pequeña escala, regido por las leyes [similares a las] de la astronomía. Jamás lo tomé de modo tan literal. Mi punto de partida fue más bien la estabilidad de la materia, un verdadero milagro desde el punto de vista de la física clásica.
Por “estabilidad” me refiero a que las mismas sustancias siempre tienen las mismas propiedades, que los mismos cristales son recurrentes, los mismos compuestos químicos, etc. En otras palabras, aun tras una serie de cambios a causa de influencias externas, un átomo de hierro siempre seguirá siendo un átomo de hierro, con las mismísimas propiedades que antes. Los principios de la mecánica clásica [o el electromagnetismo clásico] no pueden explicar esto, sin dudas no si el átomo se asemeja a un sistema planetario. La naturaleza tiene una tendencia evidente a producir ciertas formas (…) y a recrear estas formas aun cuando se las perturba o destruye. Se puede pensar incluso en la biología: la estabilidad de los organismos vivos, la propagación de formas muy complicadas que, después de todo, solo pueden existir en su totalidad. Pero la biología se concentra en estructuras de alta complejidad, sujetas a transformaciones temporales y particulares que no vienen al caso. Concentrémonos en las formas más simples que estudiamos en la física y la química. La existencia de sustancias uniformes, de cuerpos sólidos, depende de la estabilidad de los átomos; esa es justamente la razón por la que un tubo electrónico que contiene cierto gas siempre emitirá luz del mismo color, un espectro con las mismas líneas. Todo esto, lejos de ser evidente, es inexplicable en términos de los principios básicos de la física newtoniana [y maxwelliana], según la cual todos los efectos tienen causas bien determinadas y el estado presente de un fenómeno o proceso está determinado en su totalidad por aquel que lo precede inmediatamente. Este hecho me resultaba muy inquietante cuando empecé a conocer la física atómica. (Heisenberg, Physics and Beyond, trad. al inglés A. J. Pomerans, 39)
[60] La creencia en un mundo externo independiente del sujeto que lo percibe es la base de toda la ciencia natural. (Einstein, Ideas and Opinions, 266, también 270)
[61] No puedo creer que debamos abandonar, ahora y para siempre, la idea de la representación directa de la realidad física en el espacio y el tiempo. (Einstein, Ideas and Opinions, 334)
[62] Lo que ahora es particularmente importante que comprendamos es el significado profundo de esta idea misteriosa del cuanto de la acción [la constante de Planck, h = 6.62×10-27 ergio-seg]. Hasta [principios del siglo XX] el espacio y el tiempo de la física clásica o su sucesora (el espacio-tiempo de la física de la relatividad) se nos mostraban como un marco dado a priori y bastante independiente de lo que uno insertara en ella, bastante independiente en particular de los movimientos y la evolución de los cuerpos que se ubicaban en ella (…).
La verdadera relevancia del cuanto de la acción se nos reveló en particular gracias al descubrimiento de las incertidumbres de Heisenberg. (…) Hoy parece innegable que la existencia del cuanto de la acción expresa una unión nunca antes sospechada entre el marco del espacio y el tiempo y los fenómenos dinámicos que ocurren en él. La imagen del espacio y el tiempo [en la física clásica] es en esencia estática; un cuerpo, un ente físico, que posee una ubicación exacta en el tiempo y el espacio carece, por este mismo hecho, de toda propiedad evolutiva; por el contrario, un cuerpo que se desarrolla, dotado de propiedades dinámicas, no puede permanecer en realidad sujeto a ningún punto del espacio y el tiempo. Estas son consideraciones filosóficas que se remontan a Zenón. (…) Las relaciones de incertidumbre de Heisenberg parecen estar en consonancia con estas afirmaciones; nos enseñan, en efecto, que es imposible atribuir simultáneamente a un cuerpo un movimiento bien definido y un lugar bien determinado en el espacio y el tiempo. (De Broglie, Physics and Microphysics, 120-22)
[63] Cuando dos sistemas cuyos estados conocemos por sus respectivos representantes comienzan una interacción física temporal, ocasionada por fuerzas conocidas entre ellos, y luego, cuando pasado un periodo de influencia mutua los sistemas vuelven a separarse, ya no se pueden describir de la misma manera que antes, esto es, asignándole a cada uno un representante propio [independiente del otro]. No diría que es una sino la característica propia de la mecánica cuántica, aquello que la diferencia por completo de las formas clásicas de pensamiento. Por la interacción, los dos representantes (o funciones Ψ) se han entrelazado. Para revertirlo, debemos obtener más información a través de experimentos. (…) Tras recobrar uno de los representantes por observación, el otro se puede inferir simultáneamente. De aquí en más, todo este proceso ha de llamarse desentrelazamiento. Su importancia suprema radica en que es parte de todo proceso de medición (…).
Otra forma de expresar esta extraña situación es: el mejor conocimiento posible de un todo no necesariamente incluye el mejor conocimiento posible de todas sus partes, aunque se las pueda separar por completo [en el espacio] y sean, por ende, virtualmente capaces de ser “conocidas lo mejor posible”, es decir, de que cada una de ellas tenga un representante propio. La falta de conocimiento no se debe en absoluto a que el entendimiento de la interacción sea insuficiente (al menos no en el sentido de que sería posible comprenderla mejor), sino más bien a la interacción misma.
En los últimos tiempos, se ha puesto de relieve [Einstein, Podolsky y Rosen, Phys. Rev. 47 (1935), 777] el hecho obvio pero muy desconcertante de que, aun si restringimos las mediciones de desentrelazamiento a un sistema, el representante obtenido para el otro sistema no es en absoluto independiente de la selección específica de observaciones que se haga a tal efecto y que, por cierto, es completamente arbitraria. Es un tanto inquietante que la teoría admita que un sistema se pueda manipular o desviar hacia uno u otro tipo de estado a voluntad del experimentador, a pesar de que este no tenga acceso a aquel. Este trabajo no busca dar una solución a la paradoja; más bien pretende profundizarla, si es posible. (Schroedinger, “Discussion of Probability Relations Between Separated Systems”, Proc. Cambridge Philosophical Society 31.1 (enero, 1935): 555-56)
[64] Sin dudas, mataríamos a un animal si intentáramos llevar la investigación de sus órganos a un punto tal que nos permitiera describir la función que cumplen los átomos individuales en las funciones vitales (…). Resulta evidente que el mínimo de libertad que debemos otorgarle al organismo en este sentido es suficiente para permitirle, por así decir, mantener ocultos sus secretos más profundos. Según esta mirada, la existencia de la vida debe considerarse un hecho elemental que no puede explicarse, pero que debe tomarse como el punto de partida en la biología, así como el cuanto de la acción, que parece un elemento irracional desde el punto de vista de la física mecánica clásica, conforma, junto con la existencia de partículas elementales, el fundamento de la física atómica. (Niels Bohr, “Of Light and Life”, Nature 131 (1933): 421-23 y 457-59)
Biología: Darwin y el ADN
Darwin:
[65] Deberemos tratar las especies tal como aquellos naturalistas tratan los géneros, quienes admiten que los géneros son meras combinaciones artificiales por conveniencia. Quizás no sea una perspectiva alentadora, pero al menos nos veremos libres de la búsqueda fútil de la esencia desconocida e incognoscible del término especie. (El origen de las especies, 447)
Francis Crick (una reescritura coloquial de su “dogma central” de la biología molecular):
[66] El ADN hace el ARN, el ARN hace las proteínas y las proteínas nos hacen a nosotros. (Citado en Evelyn Fox Keller, The Century of the Gene, 54)
Jacob y Monod:
[67] El genoma no solo contiene una serie de modelos, sino también un programa coordinado de síntesis de proteínas y los medios para controlar su ejecución. (Francois Jacob y Jacque Monod, “Genetic regulatory mechanisms in the synthesis of proteins”, J. Molec. Biol. 3 (1961), 354)
Evelyn Fox Keller:
[68] En muchos casos, los indicadores experimentales del tipo que ya se trató pueden servirnos como verdaderas palancas: esto es, se pueden manipular de manera tal que se induzcan efectos definidos y reproducibles. (…) Hoy, con las técnicas para modificar el ADN de las plantas y los animales, que resultan en la producción confiable de ciertas proteínas nuevas o mejoradas, la ingeniería genética es una realidad. (…) Pero causa, en un sentido tan evidentemente pragmático, no puede dar cuenta ni de generalidad ni de consecuencias a largo plazo (…). (The Century of the Gene, 141-42)
G. Collingwood:
[69] En este sentido, la causa de un acontecimiento en la naturaleza es la palanca (…) con la que los seres humanos pueden manipularla. (…) La pregunta “¿Cuál es la causa del evento y?” significa en este caso “¿Cómo podemos producir o evitar y a voluntad?” (…). Una causa en este sentido [pragmático] (…) es condicional (…). Nadie intenta enumerar [las condiciones] en su totalidad. ¿Por qué habría de hacerlo? Si descubro que puedo obtener un resultado de cierta manera, puedo estar seguro de que no sería posible alcanzarlo si no se cumplieran muchas condiciones; pero, en tanto que lo obtenga, no me interesa saber cuáles son esas condiciones. Si a causa de cierto cambio en una de ellas no soy capaz de obtener el resultado, aun así no deseo saber cuáles son todas las condiciones, solo deseo saber cuál es la que cambió. (An Essay on Metaphysics, ed. Rex Martin, 296, 301, 303)
Leon Kass:
[70] En principio, todo es pasible de ser intervenido, porque todo es alterable, nada se considera respetablemente natural ni indeseablemente antinatural. (…) Los científicos modernos le han planteado un gran desafío a la noción de lo distintivamente humano. (…) Los espectaculares avances en genética y biología molecular (…) parecen forzar al hombre (…) al menos a reconsiderar de manera profunda (…) su lugar en el todo. (…) Las nociones y descubrimientos científicos subyacentes ponen en tela de juicio los fundamentos mismos de nuestra ética y los principios de nuestra forma de vida política. (Toward a More Natural Science, 11, 37, 3-4)


Leave A Comment